megapixels

When more is not always better – the deception of megapixels

/ spqr / Leave a comment

I have never liked how companies advertise cameras using megapixels. Mostly because it is quite deceptive, and prompts people to mistakenly believe that more megapixels is better – which isn’t always the case. But the unassuming amateur photographer will assume that 26MP is better than 16MP, and 40MP is better than 26MP. From a purely numeric viewpoint, 40MP is better than 26MP – 40,000,000 pixels outshines 26,000,000 pixels. It’s hard to dispute raw numbers. But pure numbers don’t tell the full story. There are two numeric criteria to consider when considering how many pixels an image has: (i) the aggregate number of pixels in the image, and (ii) the image’s linear dimensions.

Before we look at this further, I just want to clarify one thing. A sensor contains photosites, which are not the same as pixels. Photosites capture light photons, which are then processed in various ways to produce an image containing pixels. So a 24MP sensor will contain 24 million photosites, and the image produced by a camera containing this sensor contains 24 million pixels. A camera has photosites, an image has pixels. Camera manufacturers use the term megapixel likely to make things simpler, besides which megaphotosite sounds more like some kind of prehistoric animal. For simplicities sake, we will use photosite when referring to a sensor, and pixel when referring to an image.

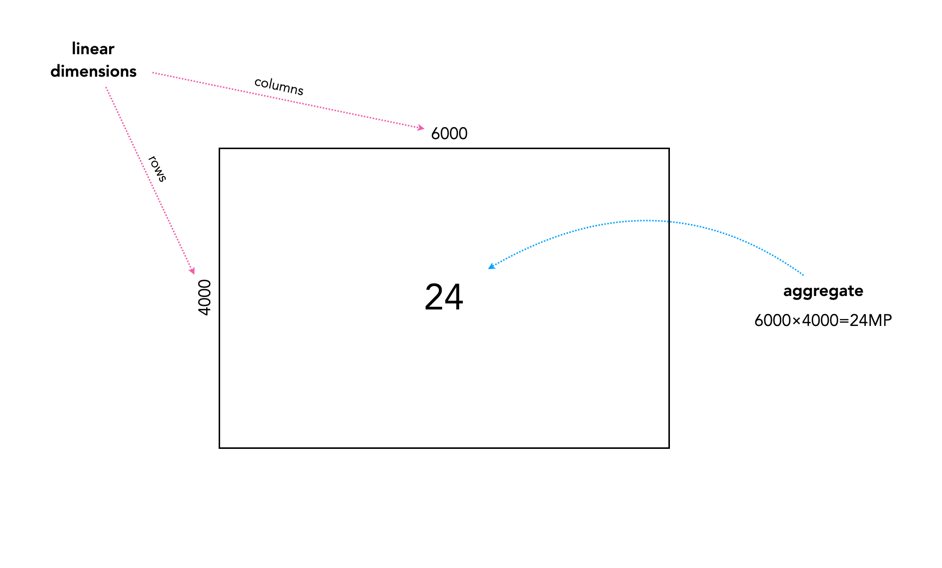
Aggregate pixels versus linear dimensions
Fig.1: Aggregate pixels versus linear dimensions

Every sensor is made up of P photosites arranged in a rectangular shape with a number of rows (r) and a number of columns (c), such that P = r×c. Typically the rectangle shape of the sensor forms an aspect ratio of 3:2 (FF, APS-C), or 4:3 (MFT). The values of r and c are the linear dimensions, which basically represent the resolution of the image in each dimension, i.e. the vertical resolution will be r, the horizontal resolution will be c. For example in a 24MP, 3:2 ratio sensor, r=4000, c=6000. The image aggregate is the number of megapixels associated with the sensor. So r×c = 24,000,000 = 24MP. This is the number most commonly associated with the resolution of an image produced by a camera. In reality, the number of photosites and the number of pixels are equivalent. Now let’s look at how this affects an image.

Doubling megapixels versus doubling linear dimensions
Fig.2: Doubling megapixels versus doubling linear dimensions

The two numbers offer different perspectives of how many pixels are in an image. For example the difference between a 16MP image and a 24MP image is a 1.5 times increase in aggregate pixels. However due to how these pixels are distributed in the image, it only adds up to a 1.25 times increase in the linear dimensions of the image, i.e. there are only 25% more pixels in the horizontal and vertical dimensions. So while upgrading from 16MP to 24MP does increase the resolution of an image, it only adds a marginal increase from a dimensional perspective. Doubling the linear dimensions of an image would require a sensor with 64 million photosites.

A visual depiction of different full-frame sensor sizes for Fuji sensors
Fig.3: A visual depiction of different full-frame sensor sizes for Fuji sensors

The best way to determine the effect of upsizing megapixels is to visualize the differences. Figure 3 illustrates various sensor sizes against a baseline 16MP – this is based on the actual megapixels found in current Fuji camera sensors. As you can see, from 16MP it makes sense to upgrade to 40MP, from 26MP to 51MP, and 40MP to 102MP. In the end, the number of pixels produced by an camera sensor is deceptive in so much as small changes in aggregate pixels does not automatically culminate in large changes in linear dimensions. More megapixels will always mean more pixels, but not necessarily better pixels.

Viewing distances, DPI and image size for printing

/ spqr / Leave a comment

When it comes to megapixels, the bottom line might be how an image ends up being used. If viewed on a digital device, be it an ultra-resolution monitor or TV, there are limits to what you can see. To view an image on an 8K TV at full resolution, we would need a 33MP image. However any device smaller than this will happily work with a 24MP image, and still not display all the pixels. Printing is however another matter all together.

The standard for quality in printing is 300dpi, or 300 dots-per-inch. If we equate a pixel to a dot, then we can work out the maximum size an image can be printed. 300 dpi is generally the “standard”, because that is the resolution most commonly used. To put this into perspective, at 300dpi, or 300 dots per 25.4mm, each pixel printed on a medium would be 0.085mm, or about as thick as 105 GSM weight paper. That means a dot area of roughly 0.007mm². For example a 24MP image containing 6000×4000 pixels can be printed to a maximum size of 13.3×20 inches (33.8×50.8cm) at 300dpi. The print sizes for a number of different sized images printed using 300dpi are shown in Figure 1.

Fig.1: Maximum printing sizes for various image sizes at 300dpi

The thing is that you may not even need 300dpi? At 300dpi the minimum viewing distance is theoretically 11.46”, whereas dropping it down to 180dpi means the viewing distance increases to 19.1” (but the printed size of an image can increase). In the previous post we discussed visual acuity in terms of the math behind it. Knowing that a print will be viewed from a minimum of 30” away allows us to determine that the optimal DPI required is 115. Now if we have a large panoramic print, say 80″ wide, printed at 300dpi, then the calculated minimum viewing distance is ca. 12″ – but it is impossible to view the entire print being only one foot away from it. So how do we calculate the optimal viewing distance, and then use this to calculate the actual number of DPI required?

The amount of megapixels required of a print can be guided in part by the viewing distance, i.e. the distance from the centre of the print to the eyes of the viewer. The golden standard for calculating the optimal viewing distance involves the following process:

  • Calculate the diagonal of the print size required.
  • Multiply the diagonal by 1.5 to calculate the minimum viewing distance
  • Multiply the diagonal by 2.0 to calculate the maximum viewing distance.

For example a print which is 20×30″ will have a diagonal of 36″, so the optimal viewing distance range from minimum to maximum is 54-72 inches (137-182cm). This means that we are no longer reliant on the use of 300dpi for printing. Now we can use the equations set out in the previous post to calculate the minimum DPI for a viewing distance. For the example above, the minimum DPI required is only 3438/54=64dpi. This would imply that the image size required to create the print is (20*64)×(30*64) = 2.5MP. Figure 2 shows a series of sample print sizes, viewing distances, and minimum DPI (calculated using dpi=3438/min_dist).

Fig.2: Viewing distances and minimum DPI for various common print sizes

Now printing at such a low resolution likely has more limitations than benefits, for example there is no guarantee that people will view the panorama from a set distance. So there likely is a lower bound to the practical amount of DPI required, probably around 180-200dpi because nobody wants to see pixels. For the 20×30″ print, boosting the DPI to 200 would only require a modest 24MP image, whereas a full 300dpi print would require a staggering 54MP image! Figure 3 simulates a 1×1″ square representing various DPI configurations as they might be seen on a print. Note that even at 120dpi the pixels are visible – the lower the DPI, the greater the chance of “blocky” features when view up close.

Fig.3: Various DPI as printed in a 1×1″ square

Are the viewing distances realistic? As an example consider the viewing of a 36×12″ panorama. The diagonal for this print would be 37.9″, so the minimum distance would be calculated as 57 inches. This example is illustrated in Figure 4. Now if we work out the actual viewing angle this creates, it is 37.4°, which is pretty close to 40°. Why is this important? Well THX recommends that the “best seat-to-screen distance” (for a digital theatre) is one where the view angle approximates 40 degrees, and it’s probably not much different for pictures hanging on a wall. The minimum resolution for the panoramic print viewed at this distance would be about 60dpi, but it can be printed at 240dpi with an input image size of about 25MP.

Fig.4: An example of viewing a 36×12″ panorama

So choosing a printing resolution (DPI) is really a balance between: (i) the number of megapixels an image has, (ii) the size of the print required, and (iii) the distance a print will be viewed from. For example, a 24MP image printed at 300dpi will allow a maximum print size of 13.3×20 inches, which has an optimal viewing distance of 3 feet, however by reducing the DPI to 200, we get an increased print size of 20×30 inches, with an optimal viewing distance of 4.5 feet. It is an interplay of many differing factors, including where the print is to be viewed.

P.S. For small prints, such as 5×7 and 4×6, 300dpi is still the best.

P.P.S. For those who who can’t remember how to calculate the diagonal, it’s using the Pythagorean Theorem. So for a 20×30″ print, this would mean:

diagonal = √(20²+30²)
         = √1300
         = 36.06

Do you need 61 megapixels, or even 102?

/ spqr / Leave a comment

The highest “native” resolution camera available today is the Phase One FX IQ4 medium format camera at 150MP. Higher than that there is the Hasselblad H6D-400C at 400MP, but it uses pixel-shift image capture. Next in line is the medium format Fujifilm GFX 100/100S at 102 MP. In fact we don’t get to full-frame sensors until we hit the Sony A7R IV, at a tiny 61MP. Crazy right? The question is how useful are these sensors for the photographer? The answer is not straightforward. For some photographic professionals these large sensors make inherent sense. For the average casual photographer, they likely don’t.

People who don’t photograph a lot tend to be somewhat bamboozled by megapixels, like more is better. But more megapixels does not mean a better image. Here are some things to consider when thinking about when considering megapixels.

Sensor size

There is a point when it becomes hard to cram any more photosites into a particular sensor – they just become too small. For example the upper bound with APC-S sensors seems to be around 33MP, with full-frame it seems to be around 60MP. Put too many photosites on a sensor and the density of the photosites increases, as the size of the photosites decreases. The smaller the photosite, the harder it is for it to collect light. For example Fuji APS-C cameras seem to tap out at around 26MP – the X-T30 has a photosite pitch of 3.75µm. Note that Fuji’s leap to a larger number of megapixels also means a leap to a larger sensor – the medium format sensor with a sensor size of 44×33mm. Compared to the APS-C sensor (23.5×15.6mm), the medium format sensor is nearly four times the size. A 51MP medium format sensor has photosites which are 5.33µm in size, or 1.42 times of size of the 26MP APS-C sensor.

The verdict? Squeezing more photosites onto the same size sensor does increase resolution, but sometimes at the expense of how light is acquired by the sensor.

Image and linear resolution

Sensors are made up of photosites that acquire the data used to make image pixels. The image resolution of an image describes the number of pixels used to construct an image. For example a 16MP sensor with a 3:2 aspect ratio has an image resolution of 4899×3266 pixels – the dimensions are sometimes termed the linear resolution. To obtain twice the image resolution we need a 64MP sensor, rather than a 32MP sensor. A 32MP sensor has 6928×4619 photosites, which results in a 1.4 times increase in the linear resolution of the image. The pixel count has doubled, but the linear resolution has not. Upgrading from a 16MP sensor to a 24MP sensor means a ×1.5 increase in the pixel count, and a ×1.2 increase in linear resolution. The transition from 16MP to 64MP is a ×2 increase in linear resolution, and a ×4 increase in the number of pixels. That’s why the difference between 16MP and 24MP sensors is also dubious (see Figure 1).

Fig.1: Different image resolutions and megapixels within an APS-C sensor

To double the linear resolution of a 24MP sensor you need a 96MP sensor. So the 61MP sensor provides about double the linear resolution of a 16MP sensor, as the 102MP sensor doubles the 24MP sensor.

The verdict? Doubling the pixel count, i.e. image resolution, does not double the linear resolution.

Photosite size

When you have more photosites, you also have to ask what their physical size is. Squeezing 41 million photosites on the same size sensor as one which previously had 24 million pixels means that each pixel will be smaller, and that comes with its own baggage. Consider for instance the full-frame camera, the full-frame Leica M10-R, which has a 7864×5200 photosites (41MP) meaning the photosite size is roughly 4.59 microns. The full-frame 24MP Leica M-E has a photosite size of 5.97 microns, so 1.7 times the area. Large photosites allow more light to be captured, while smaller photosites gather less light, so when their low signal strength is transformed into a pixel, more noise is generated.

The verdict? From the perspective of photosite size, 24MP captured on a full-frame sensor will be better than 24MP on an APS-C sensor, which in turn is better than 24MP on a M43 sensor (theoretically anyways).

Optics

Comparing the quality of a 16MP lens to a 24MP lens, we might determine that the quality, and sharpness of the lens is more important than the number of pixels. In fact too many people place an emphasis on the number of pixels and forget about the fact that light has to pass through a lens before it is captured by the sensor and converted into an image. Many high-end cameras already provide an in-camera means of generating a high-resolution images, often four times the actual image resolution – so why pay more for more megapixels? Is a 50MP full-frame sensor any good without optically perfect (or near-perfect) lenses? Likely not.

The verdict? Good quality lenses are just as important as more megapixels.

File size

People tend to forget that images have to be saved on memory cards (and post-processed). The greater the megapixels, the greater the resulting file size. A 24MP image stored as a 24-bit/pixel JPEG will be 3.4MB in size (at 1/20). As a 12-bit RAW the file size would be 34MB. A 51MP camera like the Fujifilm GFX 50S II would have a 7.3MB JPEG, and a 73MB 12-bit RAW. If the only format used is JPEG it’s probably, fine, but the minute you switch to RAW it will use way more storage.

The verdict? More megapixels = more megabytes.

Camera use

The most important thing to consider may be what the camera is being used for?

  • Website / social media photography – Full-width images for websites are optimal at around 2400×1600 (aka 4MP), blog-post images max. 1500 pixels in width (regardless of height), and inside content max 1500×1000. Large images can reduce website performance, and due to screen resolution won’t be visualized to their fullest capacity anyways.
  • Digital viewing – 4K televisions have roughly 3840×2160 = 8,294,400 pixels. Viewing photographs from a camera with a large spatial resolution will just mean they are down-sampled for viewing. Even the Apple Pro Display XDR only has 6016×3384=20MP view capacity (which is a lot).
  • Large prints – Doing large posters, for example 20×30″ requires a good amount of resolution if they are being printed at 300DPI, which is the nominal standard. So this needs about 54MP (check out the calculator). But you can get by with less resolution because few people view a poster at 100%.
  • Average prints – An 8×10″ print requires 2400×3000 = 7.2MP at 300DPI. A 26MP image will print maximum size 14×20″ at 300DPI (which is pretty good).
  • Video – Does not need high resolution, but rather 4K video at a descent frame rate.

The verdict? The megapixel amount really depends on the core photographic application.

Postscript

So where does that leave us? Pondering a lot of information, most of which the average photographer may not be that interested in. Selecting the appropriate megapixel size is really based on what a camera will be used for. If you commonly take landscape photographs that are used in large scale posters, then 61 or 102 megapixels is certainly not out of the ballpark. For the average photographer taking travel photos, or for someone taking images for the web, or book publishing, then 16MP (or 24MP at the higher end) is ample. That’s why smartphone cameras do so well at 12MP. High MP cameras are really made more for professionals. Nobody needs 61MP.

The overall erdict? Most photographers don’t need 61 megapixels. In reality anywhere between 16 and 24 megapixels is just fine.

Further Reading

Megapixels and sensor resolution

/ spqr / 1 Comment

A megapixel is 1 million pixels, and when used in terms of digital cameras, represents the maximum number of pixels which can be acquired by a camera’s sensor. In reality it conveys a sense of the image size which is produced, i.e. the image resolution. When looking at digital cameras, this can be somewhat confusing because there are different types of terms used to describe resolution.

For example the Fuji X-H1 has 24.3 megapixels. The maximum image resolution is is 6000×4000 or 24MP. This is sometimes known as the number of effective pixels (or photosites), and represents those pixels within the actual image area. However if we delve deeper into the specifications (e.g. Digital Camera Database), and you will find a term called sensor resolution. This is the total number of pixels, or rather photosites¹, on the sensor. For the X-H1 this is 6058×4012 pixels, which is where the 24.3MP comes from. The sensor resolution is calculated from sensor size and effective megapixels in the following manner:

  • Calculate the aspect ratio (r) between width and height of the sensor. The X-H1 has a sensor size of 23.5mm×15.6mm so r=23.5/15.6 = 1.51.
  • Calculate the √(no. pixels / r), so √(24300000/1.51) = 4012. This is the vertical sensor resolution.
  • Multiply 4012×1.51=6058, to determine the horizontal sensor resolution.

The Fuji X-H1 is said to have a sensor resolution of 24,304,696 (total) pixels, and a maximum image resolution of 24,000,000 (effective) pixels. So effectively 304,696 photosites on the sensor are not recorded as pixels, representing approximately 1%. These remaining pixels form a border to the image on the sensor.

Total versus effective pixels.

So to sum up there are four terms worth knowing:

  • effective pixels/megapixels – the number of pixels/megapixels in an image, or “active” photosites on a sensor.
  • maximum image resolution – another way to describe the effective pixels.
  • total photosites/pixels – the total number of photosites on a sensor.
  • sensor resolution – another way to describe the total photosites on a sensor.

¹ Remember, camera sensors have photosites, not pixels. Camera manufacturers use the term pixels because it is easier for people to understand.

Resolution of the human eye (i) pure pixel power

/ spqr / Leave a comment

A lot of visual technology such as digital cameras, and even TVs are based on megapixels, or rather the millions of pixels in a sensor/screen. What is the resolution of the human eye? It’s not an easy question to answer, because there are a number of facets to the concept of resolution, and the human eye is not analogous to a camera sensor. It might be better to ask how many pixels would be needed to make an image on a “screen” large enough to fill our entire field of view, so that when we look at it we can’t detect pixelation.

Truthfully, we may never really be able to put an exact number on the resolution of the human visual system – the eyes are organic, not digital. Human vision is made possible by the presence of photoreceptors in the retina. These photoreceptors, of which there are over 120 million in each eye, convert electromagnetic radiation into neural signals. The photoreceptors consist of rods and cones. Rods (which are rod shaped) provide scotopicvision,  are responsible for low-light vision, and are achromatic. Cones (which are con shaped) provide photopicvision, are active at high levels of illumination, and are capable of colour vision. There are roughly 6-7 million cones, and nearly 120-125 million rods.

But how many [mega] pixels is this equivalent to? An easy guess of pixel resolution might be 125 -130 megapixels. Maybe. But then many rods are attached to bipolar cells providing for a low resolution, whereas cones each have their own  bipolar cell. The bipolar cells strive to transmit signals from the photoreceptors to the ganglion cells. So there may be way less than 120 million rods providing actual information (sort-of like taking a bunch of grayscale pixels in an image and averaging their values to create an uber-pixel). So that’s not a fruitful number.

A few years ago Roger M. Clark of Clark Vision performed a calculation, assuming a field of view of 120° by 120°, and an acuity of 0.3 arc minutes. The result? He calculated that the human eye has a resolution of 576 megapixels. The calculation is simple enough:

(120 × 120 × 60 × 60) / (0.3 × 0.3) =576,000,000

The value 60 is the number of arc-minutes per degree, and the 0.3 arcmin²  is essentially the “pixel” size. A square degree is then 60×60 arc-minutes, and contains 40,000 “pixels”.  Seems like a huge number. But, as Clark notes, the human eye is not a digital camera. We don’t take snapshots (more’s the pity), and our vision system is more like a video stream. We also have two eyes, providing stereoscopic and binocular vision with the ability of depth perception. So there are many more factors than available in a simple sensor. For example, we typically move our eyes around, and our brain probably assembles a higher resolution image than is possible using our photoreceptors (similar I would imagine to how a high-megapixel image is created by a digital camera, slightly moving the sensor, and combining the shifted images).

The issue here may actually be the pixel size. In optimal viewing conditions the human eye can resolve detail as small as 0.59 arc minutes per line pair, which equates to 0.3 arc minutes. This number comes from a study from 1897 – “Die Abhängigkeit der Sehschärfe von der Beleuchtungsintensität”, written by Arthur König (translated roughly to “The Dependence of Visual Acuity on the Illumination Intensity”). A more recent study from 1990 (Curcio90) suggests a value of 77 cycles per degree. To convert this to arc-minutes per cycle, we first divide 1 by 77 and then multiply by 60 = 0.779. Two pixels define a cycle, so 0.779/2 = 0.3895, or 0.39. Now if we use 0.39×0.39 arcmin as the pixel size, we get 6.57 pixels per arcmin², versus 11.11 pixels when the acuity is 0.3. This vastly changes the value calculated to 341megapixels (60% of the previous calculation).

Clark’s calculation using 120° is also conservative, as the eyes  field of view is roughly 155° horizontally, and 135° vertically. If we used these constraints we would get 837 megapixels (0.3), or 495 megapixels (0.39). The pixel size of 0.3 arcmin² is optimal viewing – but about 75% of the population have 20/20 vision, both with and without corrective measures. 20/20 vision implies an acuity of 1 arc minute, which means a pixel size of 1×1 arcmin². This could mean a simple 75 megapixels. There are three other factors which complicate this: (i)  these calculations assume uniform  optimal acuity, which is very rarely the case, (ii) vision is binocular, not monocular, and (iii) the field of view is likely not a rectangle.

For binocular vision, assuming each eye has a horizontal field of view of 155°, and there is an overlap of 120° (120° of vision from each eye is binocular, remaining 35° in each eye is monocular). This results in an overall horizontal field of view of 190°, meaning if we use 190°, and 1 arc minute acuity we get a combined total vision of 92 megapixels. If we change acuity to 0.3 we get over 1 gigapixel. Quite a range.

All these calculations are mere musings – there are far too many variables to consider in trying to calculate a generic number to represent the megapixel equivalent of the human visual system. The numbers I have calculated are approximations only to show the broad range of possibilities based solely on a few simple assumptions. In the next couple of posts we’ll look at some of the complicating factors, such as the concept of uniform acuity.

REFS:
(Curcio90) Curcio, C.A., Sloan, K.R., Kalina, R.E., Hendrickson, A.E., “Human photoreceptor topography”, The Journal of Comparative Neurology, 292, pp.497-523 (1990)