angle of view

The real info regarding angle-of-view on iPhone cameras

/ spqr / Leave a comment

I must say, I quite like the wide lenses on the iPhone 14. It has two rear-facing cameras, an ultra-wide with a focal length of 13mm, and a 26mm wide (full-frame equiv). I don’t really want to get into reviewing these cameras, because other people have already done extensive reviews. An example of a portrait shot taken with each camera is shown below in Figure 1 (picture of the Gooderham “flatiron” Building in Toronto).

Fig.1: Example of portrait photos using both 26mm and 13mm cameras.

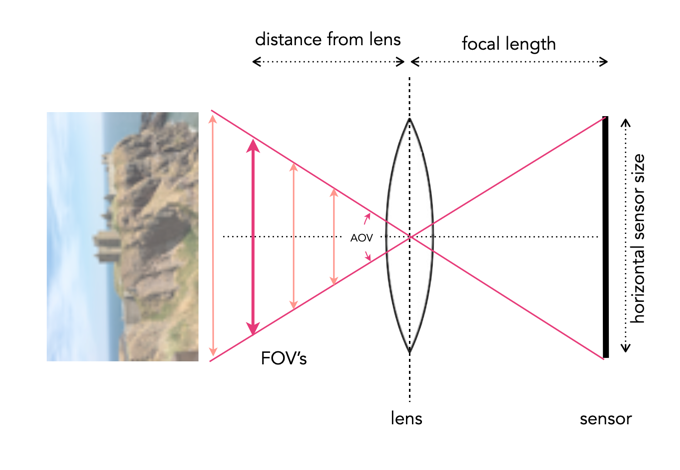
But I do want to talk briefly about the Angle of View (AOV) of these cameras. Firstly, you really have to hunt for some of this information. Apple doesn’t really talk about sensor size, or even AOV to any great extent. The most they give you is that the AOV of the ultrawide camera is 120°. But they don’t tell you the full story (maybe because most people don’t care?). It may be 120°, but only in landscape mode, and that angle describes the diagonal angle, which as I have mentioned before isn’t really that useful for most people because it is much harder to conceptualize than horizontal degrees (it’s no different to TV’s, and nobody measures a TV based on its diagonal).

Pixel countFocal lengthSensor sizef-numberAOV
landscape		Crop factor
12MP26mm (equiv.)Type 1/1.7 (9.5×7.6mm)f/1.569° (H)4.6
12MP13mm (equiv.)Type 1/3.4 (4×3mm)f/2.4108°(H)
120°(D)		8.6
iPhone 14 (rear-facing) camera specs

So the wide-angle camera has a horizontal AOV of 69°, and the ultrawide has an AOV of 108°. But this is when a photograph is taken in landscape mode. When a photograph is taken in portrait mode, the horizontal AOV defaults to the vertical AOV from landscape mode – this means 85° for the wide, and a mere 50° for the ultrawide. This concept is the same for all sensors in all cameras, because in portrait mode the width of the photo is obviously less than that of the landscape photo. In mobile devices such as the iPhone this does become a little trickier, because most photos are likely taken in portrait mode.

Examples of the AOV’s in portrait mode for each of the focal lengths as they relate to the photographs in Figure 1 are shown below in Figure 2 (along with the potential AOV’s for landscape mode).

Fig.2: A visual depiction of the portrait AOV’s associated with the photographs of Fig.1

This is really more of a specification problem, information which I wish Apple would just post instead of ignoring. Some people are actually interested in these sort of things.

The different Angle-of-View measurements

/ spqr / 2 Comments

Look at any lens spec, and they will normally talk about the angle-of-view (AOV), sometimes used interchangeably (and incorectly) with field-of-view (FOV). But there are three forms of AOV, and they can be somewhat confusing. The first form is the diagonal AOV. It is one of the most common ones found in lens literature, but it isn’t very easy to comprehend without viewing the picture across the diagonal. Next is the vertical AOV, which makes the least sense, because we generally don’t take pictures, or even visualize the vertical. Lastly is the horizontal AOV, which makes the most sense, because of how humans perceive the world in front of them.

Showing the diagonal AOV of a lens is hard to conceptualize. It’s a bit like the way TV’s are described as being, say 50″, which is the diagonal measurement. In reality through, the TV is only 43.6″ wide. Horizontal is how people generally conceptualize things. As an example of a lens, consider a 24mm full-frame lens – it has a diagonal AOV of 84°, and a horizontal AOV of 74°. This isn’t really a lot, but enough to get a little confusing. A 16mm lens that has a AOV of 180° in the vertical, may only have a horizontal AOV of 140° An example of this is shown below.

FOV and AOV

/ spqr / Leave a comment

Photography, like many fields is full of acronyms, and sometimes two terms seem to merge into one, when the reality is not the case. DPI, and PPI for instance. Another is FOV and AOV, representing Field-Of-View, and Angle-Of-View respectively. Is there a difference between the two, or can the terms be used interchangeably? As the name suggests, AOV relates to angles, and FOV measures linear distance. But look across the net and you will find a hodge-podge of different uses of both terms. So let’s clarify the two terms.

Angle-of-View

The Angle-of-view (AOV) of a lens describes the angular coverage of a scene. It can be specified as a horizontal, vertical, or diagonal AOV. For example, a 50mm lens on a 35mm film camera would have a horizontal AOV of 39.6°, a vertical AOV of 27°, and a diagonal AOV of 46.8°. It can be calculated using the following formula (calculated in degrees):

      AOV = 2 × arctan(SD / (2×FL)) × (180 / π)°

Here SD represents the dimension of the sensor (or film) in the direction being measured, and FL is the focal length of the lens. For example a full-frame sensor will have a horizontal dimension that is 36mm, so SD=36. A visual depiction of a horizontal AOV is shown in Figure 1.

Fig.1: A horizontal AOV

A short focal length will hence produce a wide angle of view. Consider the Fuji XF 23mm F1.4 R lens. The specs give it an AOV of 63.4°, if used on a Fuji camera with an APS-C sensor (23.6×15.6mm). Using this information the equation works well, but you have to be somewhat careful because manufacturers often specify AOV for the diagonal, as is the case for the lens above. The horizontal AOV is 54.3°.

Field-of-View

The Field-of-view (FOV) is a measurement of the field dimension a lens will cover at a certain distance from the lens. The FOV can be described in terms of horizontal, vertical or diagonal dimensions. A visual depiction of a horizontal FOV is shown in Figure 2.

Fig.2: A horizontal FOV

To calculate it requires the AOV and the distance to the subject/object. It can be calculated with this equation:

      FOV = 2 ( tan(AOV/2) × D )°

Here D is the distance from the object to the lens. Using this to calculate the horizontal FOV for an object 100ft from the camera, using the AOV as 0.9477138 radians (54.3°). The FOV=102 feet. It does not matter if the value of D is feet or metres, as the result will be in the same units. There is another formula to use, without the need for calculating the AOV. 

      FOV = (SD × D)/FL

For the same calculation (horizontal FOV) using SD=23.6, FL=23mm, D=100ft, the value calculated is 102ft.

Shorter focal lengths will have a higher FOV than longer focal lengths, hence the reason why wide-angle lenses have such as broad FOV, and telephoto lens have a narrow FOV. A visual depiction of a the effect of differing focal lengths is shown in Figure 3.

Fig.3: FOV changes with focal length

FOV also changes with sensor size, as the dimension of the sensor, SD, changes. A visual depiction of the effect of differing sensor sizes on FOV is shown in Figure 4. Here two different sized sensors use lenses with differing focal lengths to achieve the same FOV.

Fig.4: FOV changes with sensor size

AOV versus FOV

The AOV remains constant for a given sensor and lens, whereas the FOV varies with the distance to the subject being photographed.

Quite a good AOV/FOV visualizer can be found here.