Why are vintage super-fast lenses so expensive?

April 6, 2022January 3, 2025 / spqr / 2 Comments

In the 1940s, a lens speed of f/3.5 was quite normal, an f/2 very fast. The world first f/1.4 lens for a 35mm camera appeared in 1950, when Nikon released the NIKKOR-S 5cm f/1.4. That sparked a series of f/1.4 lenses from most manufacturers. But this wasn’t fast enough. In the world of vintage lenses, f/1.2 lenses are almost the holy grail. Fujinon was the first to introduce an f/1.2 5cm lens in 1954 for rangefinder cameras. Canon introduced a 50mm f/1.2 lens, for the Canon S series in 1956. Many manufacturers followed suit, producing one or more lenses in the decades to come. Japanese camera companies lead the way in super-fast normal lenses. Some milestones:

First f/1.2 lens (1954) – Fuji Fujinon 5cm f/1.2 (35mm rangefinder)
First f/1.2 for SLR (1962) – Canon Super-Canonmatic R 58mm f/1.2
First f/1.2 55mm lens (1965) – Nikon Nikkor-S Auto 55mm f/1.2
First f/1.2 50mm lens for SLR (1975) – Pentax SMC 50mm f/1.2

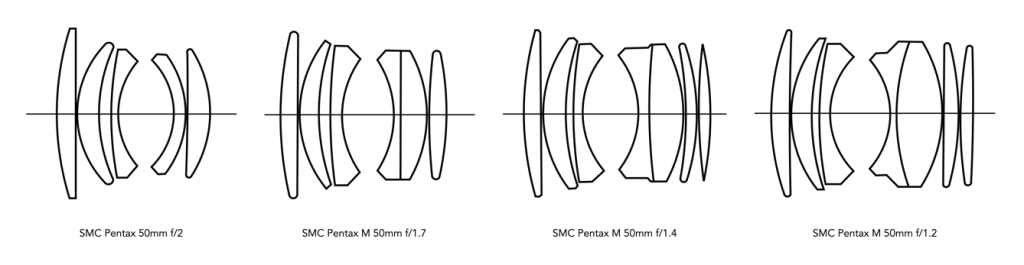
Fig.1: *The ever increasing complexities of optical elements in lenses with large apertures* from f/2 to f/1.2 *(Asahi Pentax)*

Aside from the fact that these f/1.2 lenses represent the pinnacle of wide-open lenses of the period, what makes them so expensive (both then and now)?

Rarity – Although a large number of manufacturers developed f/1.2 lenses, in may cases fewer were manufactured than slower lenses. For example, the Fujinon 5cm f/1.2 lens was made in limited amounts, less than 1000 by all accounts, but because of this ranges from $4000-20000.
Larger glass – As the speed of a lens increased, so too did the size of its optical elements. An f/1.2 lens had much more glass than say an f/2.8, e.g. a 50mm f/2.8 lens would have an effective aperture of 25mm, while an f/1.2 50mm would have one of 41.7mm. This means the optical elements had to be much larger for an f/1.2 lens.
Better glass – Larger optical elements also mean they had to be of a higher quality, with less tolerance for defects such as bubbles. Some optical elements may have been made of rare-earth metals to improve optical qualities, and reduce aberrations.
More optical elements – As lenses got faster, more elements needed to be added to counter optical aberrations.
Inner mechanisms – Larger optical elements meant one of two things for the lens housing (i.e. barrel): (i) make it a lot larger, and therefore increase the size of all the components, or (ii) make it marginally larger, and reduce the size of the mechanisms within the lens, e.g. aperture control, so they become more compact.
Complex manufacturing – Specialized glass needed new processes to ensure high manufacturing tolerances, e.g. finer levels of polishing.

Fig.2: *The ever increasing size and weight of lenses with large apertures* *(the Canon rangefinder series)*

All these elements contributed to an increase in the cost of these “revolutionary” lenses. However, although we consider them expensive now, f/1.2 lenses were always expensive. In 1957, the Canon 50mm f/1.2 rangefinder lens sold for US$250, with the Fujinon 50mm f/1.2 at $299.50 [1]. The Canon 50mm f/1.8 on the other hand sold for $125, and a Canon V with a 50mm f/1.8 lens sold for $325. A 1970 Canon price [2] list provides a better perspective, with information for the lenses for the Canon 7/7s rangefinder. The slower 50mm lens sold for $55 (f/2.8), and $120 (f/1.8), while the f/1.4 sold for $160 and the f/1.2 for $220 (the f/0.95 was the most expensive at $320). SLR lenses were cheaper, although Canon did not make a 50mm f/1.2 (until 1980), it did make a 55mm f/1.2, which sold for $165.

Note that $220 in 2022 dollars is $1608. Today, some of these lenses fetch a good price, depending on condition. The Canon 50mm f/1.2 sells for around $400-600 based on condition. The series of f/1.2 lenses made by Tomioka Kogaku circa 1970 regularly sell for between C$800-1700.

The price of nostalgia.

The Pentax (Asahi) 17mm fish-eye lens – 160 or 180°?

March 4, 2022 / spqr / 1 Comment

The closest Pentax came to a fisheye prior to the 17mm was the Takumar 18mm, which had an angle of view of 148°. In 1967, Pentax introduced the 17mm fish-eye. There are some discrepancies with whether the Asahi fish-eye lenses had an angle-of-view of 160° or 180°. During the period when Asahi Pentax produced the 17mm lens, it seems there were three versions.

Fish-eye-Takumar 17mm f/4 (1967-1971)
- This seems to be referred to in the literature as a Super-Takumar.
Super-Multi-Coated FISH-EYE-TAKUMAR 17mm f/4 (1971-1975)
SMC PENTAX FISH-EYE 17mm f/4 (1975-1985)

Many people assume every variant is 180°, but the literature such as brochures seems to tell another story. As you can see from the snippets of various catalog’s shown below, the earliest version seems to be 160°, with some transition between the Super-Takumar and Super-Multicoated being either 160° or 180°, with the later SMC versions being all 180°. What’s the real story? I haven’t been able to find out. Short of physically measuring the earlier two versions it’s hard to tell whether the early versions were indeed 160°, or was it a typo?

*Specs from various pieces of literature*

Using vintage fisheye lenses on a crop-sensor

March 2, 2022March 3, 2022 / spqr / Leave a comment

I love vintage lenses, and in the future, I will be posting much more on them. The question I want to look at here is the usefulness of vintage fish-eye lenses on crop sensors. Typically 35mm fisheye lenses are categorized into circular, and full-frame (or diagonal). A circular fisheye is typically in the range 8-10mm, with full-frame fisheye’s typically 15-17mm. The difference is shown in Figure 1.

*Fig. 1: Circular 7.5mm versus full-frame 17mm*

The problem arises with the fact that fish-eye lenses are different. So different that the projection itself can be one of a number of differing types, for example equidistant, and equisolid. That aside, using a fisheye lens on a crop-sensor format produces much different results. This of course has to do with the crop factor. An 8mm circular fisheye on a camera with an APS-C sensor will have an AOV (Angle-of-View) equivalent to a 12mm lens. A 15mm full-frame fisheye will similarly have an AOV equivalent of a 22.5mm lens. A camera with a MFT sensor will produce an even smaller image. The effect of crop-sensors on both circular and full-frame fisheye lenses is shown in Figure 2.

*Fig.2: Picture areas in circular and full-frame fisheye lenses on full-frame, and crop-sensors*

In particular, let’s look at the Asahi Super Takumar 17mm f/4 fish-eye lens. Produced from 1967-1971, in a couple of renditions, this lens has a 160° angle of view, in the diagonal, 130° in the horizontal. This is a popular vintage full-frame fisheye lens.

The effect of using this lens on a crop-sensor camera is shown in Figure 4. It effectively looses a lot of its fisheye-ness. In the case of an APS-C sensor, the 160° in the diagonal reduces to 100°, which is on the cusp of being an ultra-wide. When associated with a MFT sensor, the AOV reduces again to 75°, now a wide angle lens. Figure 4 also shows the horizontal AOV, which is easier to comprehend.

*Fig.4: The Angle-of-View of the Super-Takumar 17mm of various sensors*

The bottom line is, that a full-frame camera is the best place to use a vintage fish-eye lens. Using one on a crop-sensor will limit its “fisheye-ness”. Is it then worthwhile to purchase a 17mm Takumar? Sure if you want to play with the lens, experiment with it’s cool built-in filters (good for B&W), or are looking for a wide-angle lens equivalent, any sort of fisheye effect will never be achieved. In many circumstances, if you want a more pronounced fisheye effect on a crop-sensor, it may be better to use a modern fisheye instead.

NB: Some Asahi Pentax catalogs suggest the 17mm has an AOV of 160°, while others suggest 180°.

The different Angle-of-View measurements

February 23, 2022 / spqr / 2 Comments

Look at any lens spec, and they will normally talk about the angle-of-view (AOV), sometimes used interchangeably (and incorectly) with field-of-view (FOV). But there are three forms of AOV, and they can be somewhat confusing. The first form is the diagonal AOV. It is one of the most common ones found in lens literature, but it isn’t very easy to comprehend without viewing the picture across the diagonal. Next is the vertical AOV, which makes the least sense, because we generally don’t take pictures, or even visualize the vertical. Lastly is the horizontal AOV, which makes the most sense, because of how humans perceive the world in front of them.

Showing the diagonal AOV of a lens is hard to conceptualize. It’s a bit like the way TV’s are described as being, say 50″, which is the diagonal measurement. In reality through, the TV is only 43.6″ wide. Horizontal is how people generally conceptualize things. As an example of a lens, consider a 24mm full-frame lens – it has a diagonal AOV of 84°, and a horizontal AOV of 74°. This isn’t really a lot, but enough to get a little confusing. A 16mm lens that has a AOV of 180° in the vertical, may only have a horizontal AOV of 140° An example of this is shown below.

Fixing the “crop-factor” issue

July 29, 2021 / spqr / 3 Comments

We use the term “cropped sensor” only due to the desire to describe a sensor in terms of the 35mm standard. It is a relative term which compares two different types of sensor, but it isn’t really that meaningful. Knowing that a 24mm MFT lens “behaves” like a 48mm full-frame lens is pointless if you don’t understand how a 48mm lens behaves on a full-frame camera. All sensors could be considered “full-frame” in the context of their environment, i.e. a MFT camera has a full-frame sensor as it relates to the MFT standard.

As mentioned in a previous post, the “35mm equivalence” is used to relate a crop-factor lens to its full-frame equivalent. The biggest problem with this is the amount of confusion it creates for novice photographers. Especially as focal lengths on lenses are always the same, yet the angle-of-view changes according to the sensor. However there is a solution to the problem, and that is to stop using the focal length to define a lens, and instead use AOV. This would allow people to pick a lens based on its angle-of view, both in degrees, but also from a descriptive point of view. For example, a wide angle lens in full-frame is 28mm – its equivalent in APS-C in 18mm, and MFT is 14mm. It would be easier just to label these by the AOV as “wide-74°”.

It would be easy to categorize lenses into six core groups based on horizontal AOV (diagonal AOV in []) :

Ultra-wide angle: 73-104° [84-114°]
Wide-angle: 54-73° [63-84°]
Normal (standard): 28-54° [34-63°]
Medium telephoto: 20-28° [24-34°]
Telephoto: 6-20° [8-24°]
Super-telephoto: 3-6° [4-8°]

*Lenses could be advertised using a graphic to illustrate the AOV (horizontal) of the lens. This effectively removes the need to talk about focal length.*

They are still loosely based on how AOV related to 35mm focal lengths. For example 63° relates to the AOV of a 35mm lens, however it no longer really relates to the focal length directly. A “normal-40°” lens would be 40° no matter the sensor size, even though the focal lengths would be different (see table below). The only lenses left out of this are fish-eye lenses, which in reality are not that common, and could be put into a
specialty lens category, along with tilt-shift etc.

*Instead of brochures containing focal lengths they could contain the AOV’s.*

I know most lens manufacturers describe AOV using diagonal AOV, but this is actually more challenging for people to perceive, likely because looking through a camera we generally look at a scene from side-to-side, not corner-to-corner.

AOV	98°	84°	65°
MFT	8mm	10mm	14mm
APS-C	10mm	14mm	20mm
FF	16mm	20mm	28mm

Wide/ultra-wide angle lenses

AOV	54°	49°	40°
MFT	17mm	20mm	25mm
APS-C	24mm	28mm	35mm
FF	35mm	40mm	50mm

Normal lenses

AOV	28°	15°	10°
MFT	35mm	70mm	100mm
APS-C	45mm	90mm	135mm
FF	70mm	135mm	200mm

Telephoto lenses

The effect of crop sensors on lenses

June 18, 2021 / spqr / Leave a comment

Lenses used on crop-sensor cameras are a little different to those of full-frame cameras. Mostly this has to do with size – because the sensor is smaller, the image circle doesn’t need to be as large, and therefore less glass is needed in their construction. This allows crop-sensor lenses to be more compact, and lighter. The benefit is that for lenses like telephoto, a smaller size lens is required. A 300mm FF equivalent in MFT only needs to be 150mm. But what does focal-length equivalency mean?

Focal-Length Equivalency

The most visible effect of crop-sensors on lenses is the angle-of-view (AOV), which is essentially where the term crop comes from – the smaller sensor’s AOV is a crop of the full frame. Take a photograph with two cameras: one with a full-frame and another with an APS-C sensor, from the same position using lens with the same focal lengths. The camera with the APS-C sensor will have a more narrowed AOV. For example a 35mm lens on a FF camera has the same focal length as a FF on an MFT or APS-C camera, however the AOV will be different on each. An example of this is shown in Fig.1 for a 35mm lens (showing horizontal AOV).

Fig.1: *AOV for 35mm lenses on FF, APS-C, and MFT*

Now it should be made clear that none of this affects the focal length of the lens. The focal length of a lens remains the same – regardless of the sensor on the camera. Therefore a 50mm lens in FF, APS-C or MFT will always have a focal length of 50mm. What changes is the AOV of each of the lenses, and consequently the FOV. In order to obtain the same AOV on a cropped-sensor camera, a new lens with the appropriate focal length must be chosen.

Manufacturers of crop-sensors like to use the term “equivalent focal length“. Now this is the focal length AOV as it relates to full-frame. So Olympus says that a MFT lens with a focal length of 17mm has a 34mm FF equivalency. It has an AOV of 65° (diagonal, as per the lens specs), and a horizontal AOV of 54°. Here’s how we calculate those (21.64mm is the diagonal of the MFT sensor, which is 17.3×13mm in size):

17mm MFT lens → 2*arctan(21.64/(2*17)) = 65° (diag)
17mm MFT lens → 2*arctan(17.3/(2*17)) = 54° (hor)
34mm FF lens → 2*arctan(36/(2*34)) = 55.8° (hor)

So a lens with a 17mm focal length on a camera with a 2.0× crop factor MFT sensor would give an AOV equivalent of to that of a 34mm lens. An APS-C sensor has a crop factor of ×1.5, so a 26mm lens would be required to give an AOV equivalent of the 34mm FF lens. Figure 2 depicts the differences between 50mm FF and APS-C lenses, and the similarities between a 50mm FF lens and a 35mm APS-C lens (which give approximately the same AOV/FOV).

Fig.2: *Example of lens equivalencies: FF vs. APS-C (×1.5)*

Interchangeability of Lenses

On a side note, FF lenses can be used on crop-sensor cameras because the image circle of the FF lens is larger than the crop sensor. The reverse is however not possible, as a CS lens has a smaller image circle than a FF sensor. The picture below illustrates the various combinations of FF/MFT sensor cameras, and FF/MFT lenses.

Fig.3:*The effect of interchanging lenses between FF and crop sensor cameras.*

Of course all this is pointless if you don’t care about comparing your crop-sensor camera to a full-frame camera.

NOTE: I tend to use horizontal AOV rather than the manufacturers more typical diagonal AOV. It makes more sense because I am generally viewing a scene in a horizontal context.

FOV and AOV

April 1, 2021 / spqr / Leave a comment

Photography, like many fields is full of acronyms, and sometimes two terms seem to merge into one, when the reality is not the case. DPI, and PPI for instance. Another is FOV and AOV, representing Field-Of-View, and Angle-Of-View respectively. Is there a difference between the two, or can the terms be used interchangeably? As the name suggests, AOV relates to angles, and FOV measures linear distance. But look across the net and you will find a hodge-podge of different uses of both terms. So let’s clarify the two terms.

Angle-of-View

The Angle-of-view (AOV) of a lens describes the angular coverage of a scene. It can be specified as a horizontal, vertical, or diagonal AOV. For example, a 50mm lens on a 35mm film camera would have a horizontal AOV of 39.6°, a vertical AOV of 27°, and a diagonal AOV of 46.8°. It can be calculated using the following formula (calculated in degrees):

      AOV = 2 × arctan(SD / (2×FL)) × (180 / π)°

Here SD represents the dimension of the sensor (or film) in the direction being measured, and FL is the focal length of the lens. For example a full-frame sensor will have a horizontal dimension that is 36mm, so SD=36. A visual depiction of a horizontal AOV is shown in Figure 1.

A short focal length will hence produce a wide angle of view. Consider the Fuji XF 23mm F1.4 R lens. The specs give it an AOV of 63.4°, if used on a Fuji camera with an APS-C sensor (23.6×15.6mm). Using this information the equation works well, but you have to be somewhat careful because manufacturers often specify AOV for the diagonal, as is the case for the lens above. The horizontal AOV is 54.3°.

Field-of-View

The Field-of-view (FOV) is a measurement of the field dimension a lens will cover at a certain distance from the lens. The FOV can be described in terms of horizontal, vertical or diagonal dimensions. A visual depiction of a horizontal FOV is shown in Figure 2.

To calculate it requires the AOV and the distance to the subject/object. It can be calculated with this equation:

      FOV = 2 ( tan(AOV/2) × D )°

Here D is the distance from the object to the lens. Using this to calculate the horizontal FOV for an object 100ft from the camera, using the AOV as 0.9477138 radians (54.3°). The FOV=102 feet. It does not matter if the value of D is feet or metres, as the result will be in the same units. There is another formula to use, without the need for calculating the AOV.

      FOV = (SD × D)/FL

For the same calculation (horizontal FOV) using SD=23.6, FL=23mm, D=100ft, the value calculated is 102ft.

Shorter focal lengths will have a higher FOV than longer focal lengths, hence the reason why wide-angle lenses have such as broad FOV, and telephoto lens have a narrow FOV. A visual depiction of a the effect of differing focal lengths is shown in Figure 3.

FOV also changes with sensor size, as the dimension of the sensor, SD, changes. A visual depiction of the effect of differing sensor sizes on FOV is shown in Figure 4. Here two different sized sensors use lenses with differing focal lengths to achieve the same FOV.

AOV versus FOV

The AOV remains constant for a given sensor and lens, whereas the FOV varies with the distance to the subject being photographed.

Quite a good AOV/FOV visualizer can be found here.

The first 35mm lens

March 6, 2020January 17, 2023 / spqr / Leave a comment

With the advent of 35mm film cameras came the need to design 35mm lenses. The first still cameras designed to use 35mm film inevitably used lenses modified from use on motion-picture cameras, or microscopes. This made sense when the 35mm cine-film used the 18×24mm frame format, however these lenses only covered part of a 24×36mm frame. The figure below shows frame coverage of a cine (movie) lens versus a 35mm lens.

For instance the Tourist Multiple used a Bausch & Lomb Zeiss 4-element Tessar (50mm f / 3.5 lens), which was used on motion picture cameras.

Leitz, founded in 1869, began as a company focused on the manufacture of microscopes, and other optical instruments. When work began on the Ur-Leica, Barnack and Berek tried a number of lenses. The simplest option was the 5cm f / 3.5 Zeiss Kino-Tessar movie camera lens. The problem is that the lens could not provide a light spot able to cover the 24×36mm frame format, as it was designed for a 18×24mm format. In addition it produced vignetting not suitable for a camera. The lens they ended up using was the 6-element 42mm f / 4.5 Leitz Mikro-Summar, in a classic double-Gauss formula. This lens had a number of shortcomings, including edge blurring, and a lack of contrast.

*The Leitz Mikro-Summar* (from 1907 catalog)

The design of a new 35mm lens was the responsibility of German physicist and mathematician, Max Berek (1886-1949). The first 35mm lens developed at Leica was a 50mm f/3.5 Anastigmat. Based on the “Cooke Triplet” lens design, it had 5 elements in 3 groups. The lens was later marginally redesigned, still containing 5 elements in 3 groups, and was given the name Elmax (The name is derived from Ernst Leitz and Max Berek.). These lenses were used on the pre-production Leica-0, of which 31 were manufactured from 1920-1925.

At that time, the calculation of such a lens was still very complex. Light beam paths from points near or away from the optical axis had to be calculated for three wavelengths and seven refractive surfaces, all by hand using logarithmic tables. Leitz was granted patent No. 343086 for the Anastigmat in 1920.

The first lens formula was difficult to build, so Berek changed the design to a triplet with the last element a cemented doublet, i.e., 4 elements in 3 groups. This lens was renamed Elmar, and was subsequently manufactured for decades (1925-1961). The lens was similar to a Tessar, except for the location of the diaphragm. On the Elmar the diaphragm was located between the first and second elements, rather than the rear two elements.

The first lenses which appeared were of the fixed type used on the Leica I. From 1930-1959, the Elmar was made in a screw mount, and an M (bayonet) mount from 1954-1961. From 1930-1932 the lenses were matched with one body, after which they became interchangeable (M39 mount). The lens would evolve to have a maximum aperture of f/2.8, and a minimum aperture of f/22. .

*The Leica Elmar 50mm, with screw mount*

Specifications: (Original)
50mm f / 3.5 Elmar lens
Angle of view: 45°
No. of elements: 4
Minimum focusing distance: 1.0m
Minimum aperture: 16
Aperture range: 3.5, 4.5, 6.3, 9, 12.5, 16
Weight: 92g

Here are some links to extra info on early Leica lenses:

Why are lenses round, and photos rectangular?

July 4, 2019 / spqr / Leave a comment

Have you ever wondered why lenses are round, and photographs rectilinear? Obviously square lenses would not work, but why not round photographs? Well, lenses do indeed produce a circular image, however the quality of this image with respect to sharpness and brightness is not at all uniform. It is sharpest and brightest near the centre of the lens, becoming progressively less sharp and bright towards the outer edge of the circle. This deterioration is due to factors such as lens aberrations which become more pronounced towards the edges of the image. In terms of the photograph, only the inner, portion of the circular image should be used, hence why photographs are rectangular, or historically more square (before 35mm film).

Basically for lenses on a particular sensor, the diameter of the circle has to be larger than the diagonal of the frame. The example below shows a Full Frame 24mm×36mm sensor and its associated image circle with a diameter of 43.27mm.

This basically means that the image sensor only makes use of roughly 59% of the image circle (the sensor is 864mm², the image circle 1470mm²). Using a circular fisheye lens, or one that is smaller than the sensor, will result in a circular image. For example, using a small 16mm cinematographic lens on a full frame sensor.

In some cases, such in the case of the Leica D-LUX 6, the camera allows swapping between a bunch of aspect ratios: 16:9, 4:3, 3:2, and 1:1. This camera has a 1/1.7″ sensor (crop factor of 4.6). The actual sensor size is 3678 x 2745 pixels.

Crafting Pixels

Vintage lenses, photography and digital imagery

lens