camera

What is a crop factor?

/ spqr / 1 Comment

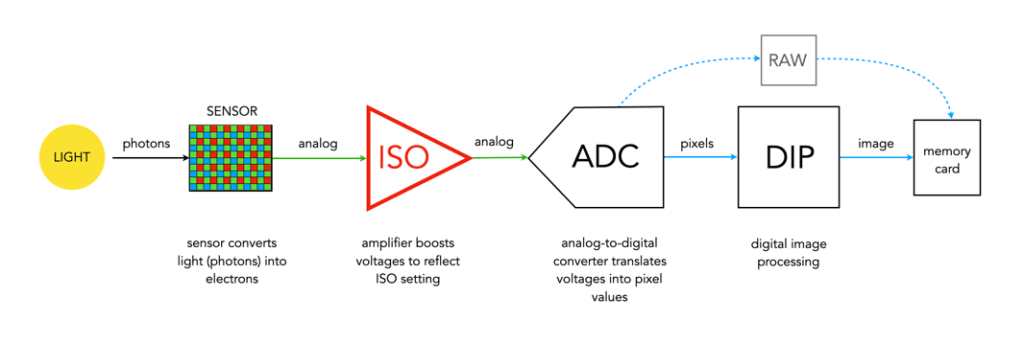
The crop factor of a sensor is the ratio of one camera’s sensor size in relation to another camera’s sensor of a different size. The term is most commonly used to represent the ratio between a 35mm full-frame sensor and a crop sensor. The term was coined to help photographers understand how existing lenses would perform on new digital cameras which had sensors smaller than the 35mm film format.

How to calculate crop factors?

It is easy to calculate a crop factor using the size of a crop-sensor in relation to a full-frame sensor. This is usually determined by comparing diagonals, i.e. full-frame sensor diagonal/cropped sensor diagonal. The diagonals can be calculated using Pythagorean Theorem. Calculate the diagonal of the crop-sensor, and divide this into the diagonal of a full-frame sensor, which is 43.27mm.

Here is an example of deriving the crop factor for a MFT sensor (17.3×13mm):

  1. The diagonal of a full-frame sensor is √(36²+24²) = 43.27mm
  2. The diagonal of the MFT sensor is √(17.3²+13²) = 21.64mm
  3. The crop factor is 43.27/21.64 = 2.0

This means a scene photographed with a MFT sensor will be smaller by a factor or 2 than a FF sensor, i.e. it will have half the physical size in dimensions.

Common crop factors

TypeCrop factor
1/2.3″5.6
1″2.7
MFT2.0
APS-C (Canon)1.6
APS-C (Fujifilm Nikon, Ricoh, Sony, Pentax)1.5
APS-H (defunct)1.35
35mm full frame1.0
Medium format (Fuji GFX)0.8

Below is a visual depiction of these crop sensors compared to the 1× of the full-frame sensor.

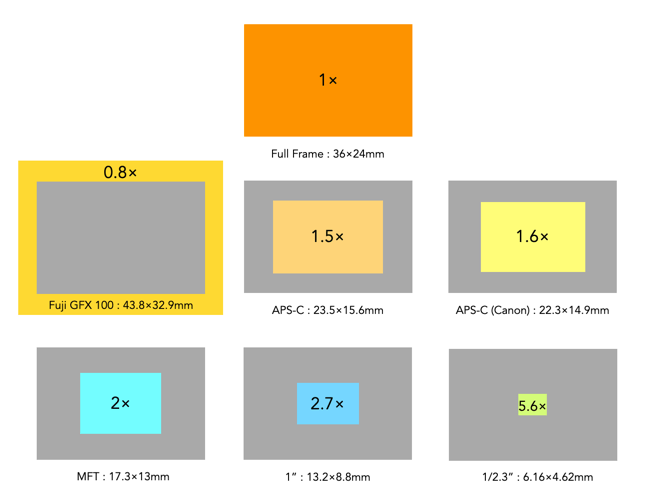
The various crop-factors per crop-sensor.

How are crop factors used?

The term crop factor is often called the focal length multiplier. That is because it is often used to calculate the “full-frame equivalent” focal length of a lens on a camera with a cropped sensor. For example, a MFT sensor has a crop factor of 2.0. So taking a MFT 25mm lens, and multiplying it by 2.0 gives 50mm. This means that a 25mm lens on a MFT camera would behave more like a 50mm lens on a FF camera, in terms of AOV, and FOV. If a 50mm mounted on a full-frame camera is placed next to a 25mm mounted on a MFT camera, and both cameras were the same distance from the subject, they would yield photographs with similar FOVs. They would not be identical of course, because they have different focal lengths which modifies characteristics such as perspective and depth-of-field.

Things to remember

  • The crop-factor is a value which relates the size of a crop-sensor to a full-frame sensor.
  • The crop-factor does not affect the focal length of a lens.
  • The crop-factor does not affect the aperture of a lens.

The low-down on crop sensors

/ spqr / 1 Comment

Before the advent of digital cameras, the standard reference format for photography was 35mm film, with frames 36×24mm in size. Everything in analog photography had the same frame of reference (well except for medium format, but let’s ignore that). In the early development of digital sensors, there were cost and technological issues with developing a sensor the same size as 35mm film. The first commercially available dSLR, the Nikon QV-1000C, released in 1988, had a ⅔” sensor with a crop-factor of 4. The first full-frame dSLR would not appear until 2002, the Contax N Digital, sporting 6 megapixels.

Using a camera with a sensor smaller presented one significant problem – the field of view of images captured using these sensors was narrower than the reference 35mm standard. When camera manufacturers started creating sensors smaller than 36×24mm, they had to create a term which described them in relation to a 35mm film-frame (full-frame). For that reason the term crop sensor is used to describe a sensor that is some percentage smaller than a full-frame sensor (sometimes the term cropped is used interchangeably). The picture a crop sensor creates is “cropped” in relation to the picture created with a full-frame sensor (using the lenses with the same focal length). The sensor does not actually cut anything, it’s just that parts of the image are simply ignored. To illustrate what happens in a full-frame versus a cropped sensor, consider Fig.1.

Fig.1: A visual depiction of full-frame versus crop sensor in relation to the 35mm image circle.

Lenses project a circular image, the “image circle”, but a sensor only records a rectangular portion of the scene. A full-frame sensor, like the one from the Leica SL2 captures a large portion of the 35mm lens circle, whereas the Micro-Four-Thirds cropped sensor of the Olympus OM-D E-M1, only captures the central portion of the lens – the rest of the image falls outside the scope of the sensor (the FF sensor is shown as a dashed box). While crop-sensor lenses are smaller than those of full-frame cameras, there are limits to reducing their size from the perspective of optics, and light capture. Fig.2 shows another perspective on crop sensors based on a real scene, comparing a full-frame sensor to an APS-C sensor (assuming the same “size” lenses, say 50mm).

Fig.2: Viewing full-frame versus crop (APS-C)

The benefits of crop-sensors

  • Crop-sensors are smaller than full-frame sensors, therefore the cameras are generally smaller. This means cameras are generally smaller in dimensions and weigh less.
  • The cost of crop-sensor cameras, and the cost of their lenses is generally lower than FF.
  • A smaller size of lens is required. For example, a MFT camera only requires a 150mm lens to achieve the equivalent of a 300mm FF lens, in terms of field-of-view.

The limitations of crop-sensors

  • Lenses on a crop-sensor camera with the same focal-length as those on a full-frame camera will generally have a smaller AOV. For example a FF 50mm lens will have an AOV=39.6°, while a APS-C 50mm lens would have an AOV=26.6°. To get a similar AOV on the cropped sensor APS-C, a 33mm equivalent lens would have to be used.
  • A cropped sensor captures less of the lens image circle than a full-frame.
  • A cropped sensor captures less light than a full-frame (which has larger photosites which are more sensitive to light).

Common crop-sensors

A list of the most common crop-sensor sizes currently used in digital cameras, as well as the average sensor sizes (sensors from different manufacturers can differ by as much as 0.5mm in size), and example cameras is summarized in Table 1. A complete list of sensor sizes can be found here. Smartphones are in a league of their own, and usually have small sensors of the type 1/n”. For example the Apple iPhone 12 Pro max has 4 cameras – the tele camera uses a 1/3.4″ (4.23×3.17mm) sensor, and the tele camera a 1/3.6″ sensor (4×3mm).

TypeExample Cameras
1/2.3″6.16×4.62mmSony HX99, Panasonic Lumix DC-ZS80, Nikon Coolpix P950
1″13.2×8.8mmCanon Powershot G7X M3, Sony X100 VII
MFT / m43 17.3×13mmPanasonic Lumix DC-G95, Olympus OM-D E-M1 Mark III
APS-C (Canon)23.3×14.9mmCanon EOS M50 Mark II
APS-C 23.5×15.6mmRicoh GRIII, Fuji X-E3, Sony α6600, Sigma sd Quattro
35mm Full Frame 36×24mmSigma fpL, Canon EOS R5, Sony α, Leica SL2-S, Nikon Z6II
Medium format44×33mmFuji GFX 100
Table 1: Crop sensor sizes.

Figure 3 shows the relative sizes of three of the more common crop sensors: APS-C (Advanced Photo System type-C), MFT (Micro-Four-Thirds), and 1″, as compared to a full-frame sensor. The APS-C sensor size is modelled on the Advantix film developed by Kodak, where the Classic image format had a size of 25.1×16.7mm.

Fig.3: Examples of crop-sensors versus a full-frame sensor.

Defunct crop-sensors

Below is a list of sensors which are basically defunct, usually because they are not currently being used in any new cameras.

TypeSensor sizeExample Cameras
1/1.7″7.53×5.64mmNikon Coolpix P340 (2014), Olympus Stylus 1 (2013), Leica C (2013)
2/3″8.8×6.6mmFujifilm FinePix X10 (2011)
APS-C Foveon 20.7×13.8mmSigma DP series (2006-2011)
APS-H Foveon26.6×17.9mmSigma sd Quattro H (2016)
APS-H27×18mmLeica M8(2006), Canon EOS 1D Mark IV (2009)
Table 2: Defunct crop sensor sizes.

From photosites to pixels (i) – the process

/ spqr / 4 Comments

We have talked briefly about digital camera sensors work from the perspective of photosites, and digital ISO, but what happens after the light photons are absorbed by the photosites on the sensor? How are image pixels created? This series of posts will try and demystify some of the inner workings of a digital camera, in a way that is understandable.

A camera sensor is typically made up of millions of cavities called photosites (not pixels, they are not pixels until they are transformed from analog to digital values). A 24MP sensor has 24 million photosites, typically arranged in the form of a matrix, 6000 pixels wide by 4000 pixel high. Each photosite has a single photodiode which records a luminance value. Light photons enter the lens and pass through the lens aperture before a portion of light is allowed through to the camera sensor when the shutter is activated at the start of the exposure. Once the photons hit the sensor surface they pass through a micro-lens attached to the receiving surface of each of the photosites, which helps direct the photons into the photosite, and then through a colour filter (e.g. Bayer), used to help determine the colour of pixel in an image. A red filter allows red light to be captured, green allows green to be captured and blue allow blue light in.

Every photosite holds a specific number of photons (sometimes called the well depth). When the exposure is complete, the shutter closes, and the photodiode gathers the photons, converting them into an electrical charge, i.e. electrons. The strength of the electrical signal is based on how many photons were captured by the photosite. This signal then passes through the ISO amplifier, which makes adjustments to the signal based on ISO settings. The ISO uses a conversion factor, “M” (Multiplier) to multiply the tally of electrons based on the ISO setting of the camera. For higher ISO, M will be higher, requiring fewer electrons.

Photosite to pixel

The analog signal then passes on to the ADC, which is a chip that performs the role of analog-to-digital converter. The ADC converts the analog signals into discrete digital values (basically pixels). It takes the analog signals as input, and classifies them into a brightness level (basically a matrix of pixels). The darker regions of a photographed scene will correspond to a low count of electrons, and consequently a low ADU value, while brighter regions correspond to higher ADU values. At this point the image can follow one (or both) of two paths. If the camera is set to RAW, then information about the image, e.g. camera settings, etc. (the metadata) is added and the image is saved in RAW format to the memory card. If the setting is RAW+JPEG, or JPEG, then some further processing may be performed by way of the DIP system.

The “pixels” passes to the DIP system, short for Digital Image Processing. Here demosaicing is applied, which basically converts the pixels in the matrix into an RGB image. Other image processing techniques can also be applied based on particular camera settings, e.g. image sharpening, noise reduction, etc. is basically an image. The colour space specified in the camera is applied, before the image as well as its associated meta-data is converted to JPEG format and saved on the memory card.

Summary: A number of photons absorbed by a photosite during exposure time creates a number of electrons which form a charge that is converted by a capacitor to a voltage which is then amplified, and digitized resulting in a digital grayscale value. Three layers of these grayscale values form the Red, Green, and Blue components of a colour image.

The facts about camera aspect ratio

/ spqr / Leave a comment

Digital cameras usually come with the ability to change the aspect ratio of the image being captured. The aspect ratio has a little to do with the size of the image, but more to do with its shape. The aspect ratio describes the relationship between an image’s width (W) and height (H), and is generally expressed as a ratio W:H (the width always comes first). For example a 24MP sensor with 6000×4000 pixels has an aspect ratio of 3:2.

Choosing a different sized aspect ratio will change the shape of the image, and the number of pixels stored in it. When using a different aspect ratio, the image is effectively cropped with the pixels outside the frame of the aspect ratio thrown away. 

The core forms of aspect ratios.

The four most common examples of aspect ratios are:

  • 4:3
    • Used when photos to be printed are 5×7″, or 8×10″.
    • Quite good for landscape photographs.
    • The standard ratio for MFT sensor cameras.
  • 3:2
    • The closest to the Golden Ratio of 1.618:1, which makes things appear aesthetically pleasing.
    • Corresponds to 4×6″ printed photographs.
    • The default ratio for 35mm cameras, and many digital cameras, e.g FF, APS-C sensors.
  • 16:9
    • Commonly used for panarama’s, or cinematographic purposes.
    • The most common ratio for video formats, e.g. 1920×1080
    • The standard aspect ratio of HDTV and cinema screens.
  • 1:1
    • Used for capturing square images, and to simplify scenes.
    • The standard ratio for many medium-format cameras.
    • Commonly used in social media, e.g. Instagram.

How an aspect ratio appears on a sensor is dependent on the sensors default aspect ratio.

Aspect ratios visualized on different sensors.

Analog 35mm cameras rarely had the ability to change the aspect ratio. One exception to the rule is the Konica Auto-Reflex, a 35mm camera with the ability to switch between full and half-frame (18×24mm) in the middle of a roll of film. It achieved this by moving a set of blinds in to change the size of the exposed area of the film plane to half-frame.

Use of the camera in Hitchcock’s “Rear Window”

/ spqr / 10 Comments

Last week I watched Rear Window, an Alfred Hitchcock directed thriller from 1954 starring James Stewart and Grace Kelly. The story follows photojournalist, L.B. “Jeff” Jefferies, who breaks his leg while shooting an action shot at a car race (supposedly working for LIFE Magazine). Confined to a wheelchair in his New York apartment, he spends time watching the occupants of neighbouring apartments through his apartments rear window, as they go about their daily lives.  He begins to suspect that a man across the courtyard may have murdered his wife. Jeff enlists the help of his high society fashion-consultant girlfriend Lisa Freemont and his visiting nurse Stella to investigate. It’s a great movie from a period when life was likely a little simpler than it is now.

For the early part of the movie, Jeff is just looking out the window, bored with being confined to his apartment while his cast covered leg recovers. When he deduces something is amiss across the courtyard, he pulls out his camera, with its telephoto lens to view the scene a little closer. The courtyard was supposedly 98′ wide and 185′ in length.

Part of the courtyard.

The 35mm film camera used by Jeff is an Exakta VX Ihagee Dresden, with the Exakta logo covered by a piece of black material in the movie. Why choose the Exakta? In the time the film was shot, there were really only three 35mm camera systems with global recognition: Leica, Contax, and Exakta. Hitchcock could have used a Leica with a reflex housing for the telephoto lens (e.g. Visoflex II), but a solution with a one-eyed reflex with a prism viewfinder was more elegant. Why was the brand covered with black tape? To cover up its East German / Communist origins? This may have played a role, but more likely just an avoidance of advertising in film.

The Exakta is an interesting choice of camera for the period, made by Ihagee Kamerawerk Steenbergen & Co, Dresden, in former East Germany and was produced between 1951-56. The Exakta is notable as being the first ever Single Lens Reflex (SLR) camera for both 127 roll film (1933), and 135 format 35mm film (1936). It’s not surprising that Jeff was using a Exakta, as before Japanese started to dominate the camera market the Exakta dominated the market, capturing perhaps 95% of SLR sales (they did kind of invent the SLR in 1936). The lens being used on the camera is a Kilfitt Fern-Kilar f/5.6 400mm telephoto lens.

The Exakta VX

There are a number of things that are of interest with the use of the camera. I know this is a movie, and the camera was used as a prop, but here goes. Firstly, as a press photographer, it is unlikely he would have used a 400mm lens. Jeff’s character was supposedly based on war photographer Robert Capa, used a Contax II with a 50mm lens. (Ironically Capa was killed covering the First Indochina War in 1954, which is where Jeff’s editor wanted to send him). A 400mm lens would be more useful for a sports photographer shooting field based sports like football (soccer) or a bird watcher. The lens Jefferies uses to take the photograph on the racetrack is clearly a wide-angle (and frankly taken from a very dangerous viewpoint).

Is Jeff pushing the shutter button?

Next there is the issue of the view through the lens itself, which it seems is solely for cinematic effect. I know from a cinematography point-of-view, Hitchcock was trying to imply that the view was through a camera, showing a circular view, but camera views are rectangular. Next there is the issue of the “focal length” of the lens, which seems to be quite flexible. There are two scenes (shown below) taken seconds apart in Thorwald’s apartment, and viewed through the Kilfitt Fern-Kilar 400mm lens. One shows a close-up of Lisa’s hand behind her back (showing where she has slipped on the victim’s wedding ring). This would mean that the 400mm lens had the ability to zoom, which was not possible (and likely act like a 800-1200mm lens). There is also the issue of light intensity, which doesn’t seem to change, even though it is nighttime. The wonders of artistic license.

Two shots, seconds apart, taken with the 400mm lens.

The field-of-view for the 400mm lens is about right for most shots, at 8-9 feet horizontally, and 5-6 feet vertically. At times it looks as though Jeff is taking photos, however the shutter release button is on the photographers left side of the camera, so from this we know he did not take any photographs. In addition, Jeff never actually cocks the shutter, which is a requirement for looking through the viewfinder – the mirror stays up after exposure, so viewfinder is dark, cocking the shutter returns the mirror to normal position (and transports the film to the next exposure).

Lars Thorwald, shown through the framed camera shot, and approximates the FOV of the lens quite well.

Which leads us to the issue of photographs. why would a photojournalist, who takes photographs for a living, not take any photographs of things happening across the courtyard? If he would have taken some photographs, then he would of at least had pictures of suspicious behaviour to show his friend Det. Lt. Doyle. But not once did we hear Jeffries depress the shutter button (and you would hear it because it is noisy). He may have taken photographs at other times, but not during the setting in the movie.

P.S. The lens was manufactured by Heinz Kilfitt Optische Fabrik (1946-64) from Munich (West Germany). Kilfitt was an innovative lens maker, producing the world’s first 35mm macro lens, the Kilfitt 4 cm f/3.5 Makro-Kilar in 1955.

Further reading:

Tracking Down and Testing the Camera from ‘Rear Window’ (1954), Thomas Bloomfield (PetaPixel, 2024)

Why do buildings lean? (the keystone effect)

/ spqr / 3 Comments

Some types of photography lend themselves to inherent distortions in the photograph, most notably those related to architectural photography. The most prominent of these is the keystone effect, a form of perspective distortion which is caused by shooting a subject at an extreme angle, which results in converging vertical (and also horizontal) lines. The name is derived from the archetypal shape of the distortion, which is similar to a keystone, the wedge-shaped stone at the apex of a masonry arch.

keystone effect in buildings
Fig.1: The keystone effect

The most common form of keystone effect is a vertical distortion. It is most obvious when photographing man-made objects with straight edges, like buildings. If the object is taller than the photographer, then an attempt will be made to fit the entire object into the frame, typically by tilting the camera. This causes vertical lines that seem parallel to the human visual system to converge at the top of the photograph (vertical convergence). In photographs containing tall linear structures, it appears as though they are “falling” or “leaning” within the picture. The keystone effect becomes very pronounced with wide-angle lenses.

Fig.2: Why the keystone effect occurs

Why does it occur? Lenses are designed to show straight lines, but only if the camera is pointed directly at the object being photographed, such that the object and image plane are parallel. As soon as a camera is tilted, the distance between the image plane and the object is no longer uniform at all points. In Fig.2, two examples are shown. The left example shows a typical scenario where a camera is pointed at an angle towards a building so that the entire building is in the frame. The angle of both the image plane and the lens plane are different to the vertical plane of the building, and so the base of the building appears closer to the image plane than the top, resulting in a skewed building in the resulting image. Conversely the right example shows an image being taken with the image plane parallel to the vertical plane of the building, at the mid-point. This is illustrated further in Fig.3.

Fig.3: Various perspectives of a building

There are a number of ways of alleviating the keystone effect. The first method involves the use of specialized perspective control and tilt-shift lenses. The best way to avoid the keystone effect is to move further back from the subject, with the reduced angle resulting in straighter lines. The effects of this perspective distortion can be removed through a process known as keystone correction, or keystoning. This can be achieved in-camera using the cameras proprietary software, before the shot is taken, or in post processing on mobile devices using apps such as SKRWT. It is also possible to perform the correction with post-processing using software such as Photoshop.

Fig.4: Various keystone effects

What happens to “extra” photosites on a sensor?

/ spqr / Leave a comment

So in a previous post we talked about effective pixels versus total photosites, i.e. the effective number of pixels in a image (active photosites on a sensor) is usually smaller than the total number of photosites on a sensor. That leaves a small number of photosites that don’t contribute to forming an image. These “extra” photosites sit beyond the camera’s image mask, and so are shielded from receiving light. But they are still useful.

These extra photosites receive a signal that tells the sensor how much dark current (unwanted free electrons generated in the CCD due to thermal energy) has built up during an exposure, essentially establishing a reference dark current level. The camera can then use this information to compensate for how the dark current contributes to the effective (active) photosites by adjusting their values (through subtraction). Light leakage may occur at the edge of this band of “extra” photosites, and these are called “isolation” photosites. The figure below shows the establishment of the dark current level.

Creation of dark current reference pixels

Camera companies – what’s in a name?

/ spqr / Leave a comment

Ever wonder where some of the camera/photographic companies got their names? Many are named for their founders: Hasselblad, Mamiya, Schneider, Voigtlander, Zeiss etc. Sometimes names are hard to pronounce, so acronyms are better: Chinon (from Chino), Cokin (from Coquin), Konica (from Konishi), Tamron (from Tamura). Leica is one of the oldest, using “Lei” from the name of the company founder, and “ca” from camera. Here are how some of the other leaders in the photograhic industry got their names…

AGFA – The name is built on the initials of the firms original German name – Actien-Gesellschaft für Anilin-Fabrikation, founded in 1867. 

CANON – Originally called Seikikogaku Kenkyujo (Precision Optical Industry Co. Ltd.), founded in 1934. The first 35mm camera produced were named, Kwanon, after the Buddhist deity of mercy. The initial Kwanon logo included an image of the goddess with 1,000 arms and flames. In 1935 they registered the name “CANON”, which seems like an Anglicization of Kwanon.

CONTAX – The first four letters derive from Contessa, a German maker of sheet-film cameras taken over by Zeiss-Ikon in 1926. The “AX” is a suffix common to German camera names, although some suggest is comes from another of Zeiss’s cameras the Tenax.

COSINA – Possibly an Anglicized version of the company’s Japanese name Kabushiki-gaisha Koshina, founded in 1959. The first part of the name is a reference to the Koshi area within Nakano, where the founder came from; while the “NA” represents Nakano.

ILFORD – Initially founded in 1879 in Ilford, UK, the Britannia Works Company, it was changed in 1902 to take on the name of the town.

KODAK – The name came from the first simple roll film cameras produced by Eastman Dry Plate Company in 1888. It had no real meaning. 

MINOLTA – The name is derived from the Japanese phrase describing the time of the rice harvest. Minoru refers to rice in its harvestable state, and ta is a rice field. The name also has a Western meaning, as an acronym for Machinery and Instruments Optical by Tashima. Minolta’s ROKKOR lenses are named for the mountains Rokko, near the company’s Osaka headquarters. 

NIKON – When founded in 1917, the company was called Nippon Kōgaku Kōgyō Kabushikigaisha. The name Nikon dates from 1946. Originally the suggestion was Nikko, an acronym made from Nippon Kogaku (Japan Optical Co.). However it was believed the name sounded too weak, so an N was added to the end.

OLYMPUS – The company was originally called Takachiho Manufacturing. Takachiho is a mountain in southwest Japan where the gods are believed to have lived and is analogous to Olympus, home to the gods in Greek mythology. Zuiko translates as “light of god”. 

PENTAX – Founded in 1919 as Asahi Kogaku Goshi Kaisha. Marketed as the Asahi Optical Co., Asahi means “rising sun”. Pentax is a combination of “PENTA” from Pentaprism, and “X” from Contax. It was originally a registered trademark of the East German VEB Zeiss Ikon and acquired by the Asahi Optical company in 1957.

POLAROID – Originally called Land-Wheelwright Laboratories, the company was renamed Polaroid after its first product (1937), a polarizing material used in military instruments and sunglasses. 

RICOH – An Anglicized acronym formed from the original Japanese name for the company, RIKagaku KOgyo, setup by the Institute for Physical and Chemical Research in 1936. Ricoh is also a homonym of the Japanese word for smart, rikoh. 

ROLLEI – Originally called the Werkstatt für Feinmechanik und Optik Franke & Heidecke when it was founded in 1920, the name Rollei was derived from the Roll-film Heidoscop, a stereo camera. 

TOKINA – Established in 1950 as Tokyo Optical Equipment Manufacturing. In the 1970s, the company began manufacturing lenses under its own brand Tokina. The prefix “TO” refers to Tokyo, the suffix “kina” is a Germanization of the Italian word for cinema, cine. 

VIVITAR – Named originally for its founders Ponder & Best, this US company imported a variety of camera brands, including Olympus, and Mamiya. When it started sourcing its own equipment a new name was created, based on the Latin vivere (to live), and the ar/tar suffix common to many of the prominent lenses such as Ektar, and Tessar. 

YASHICA – Originally called Yashima Optical Industries, when founded in 1949. Yashica is a combination of “YASHI” from Yashima, and “CA” for camera, similar to Leica.

Why camera sensors don’t have pixels

/ spqr / Leave a comment

The sensor in a digital camera is equivalent to a frame of film. They both capture light and use it to generate a picture, it is just the medium which changes: film uses light sensitive particles, digital uses light sensitive diodes. These specks of light work together to form a cohesive continuous tone picture when viewed from a distance. 

One of the most confusing things about digital cameras is the concept of pixels. They are confusing because some people think they are a quantifiable entity. But here’s the thing, they aren’t. Typically a pixel, short for picture element, is a physical point in an image. It is the smallest single component of an image, and is square in shape – but it is just a unit of information, without a specific quantity, i.e. a pixel isn’t 1mm2. The interpreted size of a pixel depends largely on the device it is viewed on. The terms PPI (pixels per inch) and DPI (dots per inch) were introduced to relate the theoretical concept of a pixel to real-world resolution. PPI describes how many pixels there are in an image per inch of distance. DPI is used in printing, and varies from device to device because multiple dots are sometimes needed to create a single pixel. 

But sensors don’t really have “pixels”. They have an array of cavities, better known as “photosites”, which are photo detectors that represent the pixels. When the shutter opens, each photosite collects light photons and stores them as electrical signals. When the exposure ends, the camera then assesses the signals and quantifies them as digital values, i.e. the things we call pixels. We tend to use the term pixel interchangeably with photosite in relation to the sensor because it has a direct association with the pixels in the image the camera creates. However a photosite is physical entity on the sensor surface, whereas pixels are abstract concepts. On a sensor, the term “pixel area” is used to describe the size of the space occupied by each photosite on the sensor. For example, a Fuji X-H1 has a pixel area of 15.05 µm² (micrometres²), which is *really* tiny.

A basic photosite

NB: Sometimes you may see photosites called “sensor elements”, or sensels.