The basics of human perception underpin the colour theory used in devices like digital cameras. The RGB colour model is based partly on the Young-Helmholtz theory of trichromatic colour vision, developed by Thomas Young, and Hermann von Helmholtz in the 19th century, the manner in which the human visual system gives rise to the theory of colour. In 1802, Young postulated the existence of three types of photoreceptors in the eye, each sensitive to a particular range of visible light. Helmholtz further developed the theory in 1850, suggesting the three photoreceptors be classified into short, middle and long according to their response to wavelengths of light striking the retina. In 1857 James Maxwell used linear algebra to prove the Young-Helmholtz theory. Some of the first experiments colour photography using the concept of RGB were made by Maxwell in 1861. He created colour images by combining three separate photographs, each taken with a red, green, and blue colour-filter.

In the early 20th century the CIE set out to create a comprehensively quantify the human perception of colour. This was based on experimental work done by William David Wright and John Guild. The results of the experiments were summarized by the standardized CIE RGB colour matching functions for R, G, and B. The name RGB stems from the fact that red, green, and blue primaries can be thought of as the basis for a vector representing a colour. Devices such as digital cameras have been designed to approximate the spectral response of the cones of the human eye. Before light photons are captured by a camera sensors photosites they pass through red, green or blue optical filters which mimic the response of the cones. The image that is formed at the other end of the process is encoded using RGB colour space information.

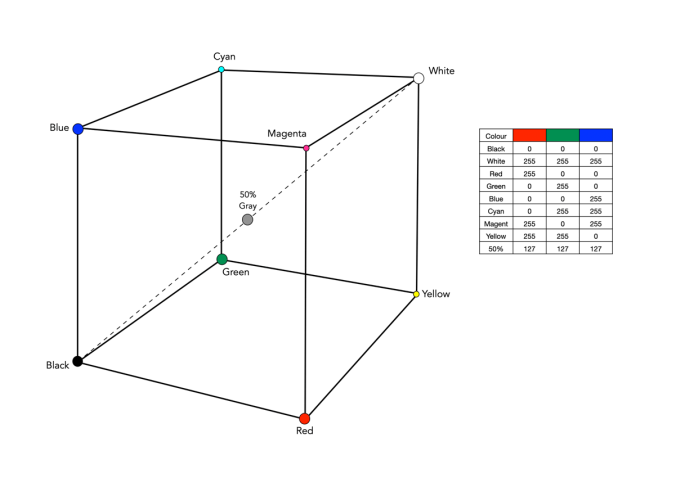
The RGB colour model is one in which colours are represented as combinations of the three primary colours: red (R), green (G), and blue (B). RGB is an additive colour model, which means that a colour is formed by mixing various intensities of red, green and blue light. The collection of all the colours obtained by such a linear combination of red, green and blue forms a cube shaped colour space (see Fig.1). Each colour, as described by its RGB components, is represented by a point that can be found either on the surface or inside the cube.

The cube, as shown in Fig.1, shows the primary (red, green, blue), and secondary colours (cyan, magenta, yellow), all of which lie on the vertices of the colour cube. The corner of RGB colour cube that is at the origin of the coordinate system corresponds to black (R=G=B=0). Radiating out from Black are the three primary coordinate axes, Red, Green, and Blue. Each of these range from 0 to C_max, where C_max is typically 255 for a 24-bit colour space (8-bits each for R, G, and B). The corner of the cube that is diagonally opposite to the origin represents white (R=G=B=255). Each of these 8-bit colours contains 256 values, so the total amount of colours which can be produced is 256³, or 16,777,216 colours. Sometimes the values are normalized between 0 and 1, and the colour cube is called the unit cube. The diagonal (dashed) line connecting black and white corresponds to all the gray colours between black and white, which is also known as gray axis. Grays are formed when all three components are equal, i.e. R=G=B. For example the 50% gray is (127,127,127).

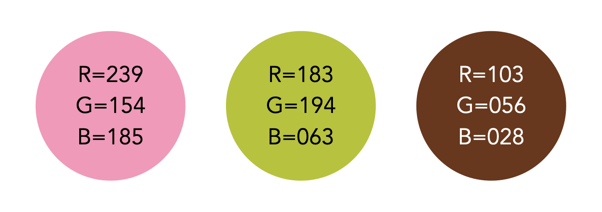
Figure 2 illustrates an RGB cube for a colour image. Notice that while the pink colour of the sky looks somewhat uniform in the image, it is anything, showing up as a swath of various shades of pink in the RGB cube. There are 275,491 unique colours in the Fig.2 image. Every possible colour corresponds to a point within the RGB colour cube, and is of the form: Cxyz = (Rx,Gy,Bz). For example Fig.3 illustrates three colours extracted from the image in Fig.2.

The RGB colour model has a number of benefits:

• It is the simplest colour model.
• No transformation is required to display data on a screen, e.g. images.
• It is a computationally practical system.
• The model is very easy to implement.

But equally it has a number of limitations:

• It is not a perceptual model. In perceptual terms, colour and intensity are distinct from one another, but the R, G, and B components each contain both colour and intensity information. This makes it challenging to perform some image processing operations in RGB space.
• It is psychologically non-intuitive, i.e. not able to determine what a particular RGB colour corresponds to in the real world, or what RGB means in a physical sense.
• It is non-uniform, i.e. it is impossible to evaluate the perceived differences between colours on the basis of distance in RGB space (the cube).
• For the purposes of image processing, the RGB space is often converted to another colour space by means of some non-linear transformation.

The RGB colour space is commonly used in imaging devices because of its affinity with the human visual system. Two of the most commonly used colour spaces derived from the RGB model are sRGB and Adobe RGB.